Das Collatz-Problem (oft auch 3n+1-Problem genannt) ist eine der bekanntesten offenen Fragen in der Mathematik – einfach zu formulieren, aber extrem schwer zu beweisen.
Regel: Wenn die Zahl gerade ist, teile durch 2; wenn sie ungerade ist, rechne 3n+1.
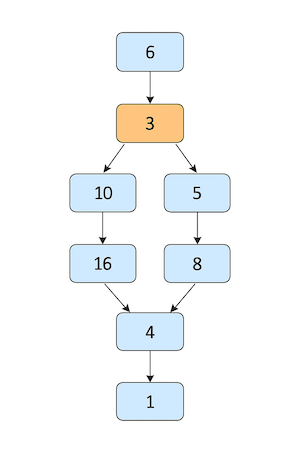
Beispiel: 6 wird zu 3, dann 10, 5, 16, 8, 4, 2, 1.
Beobachtung: Alle bisher geprüften Zahlen enden bei 4–2–1.
Frage: Niemand weiß, ob das für alle Zahlen gilt.
Schwierigkeit: Die Mischung aus Teilen, Multiplizieren und Plus macht das Verhalten unberechenbar.
Forschung: Es ist einfach aufzuschreiben, aber bis heute nicht bewiesen.
Die Regel
Du startest mit einer ganzen Zahl n>0n>0:
- Wenn nn gerade ist, rechne n/2n/2.
- Wenn nn ungerade ist, rechne 3n+13n+1.
Dann nimm das Ergebnis und wiederhole den Prozess.
Beispiel mit n=6n=6:6→3→10→5→16→8→4→2→16→3→10→5→16→8→4→2→1
Am Ende kommt man immer bei der Schleife 4 → 2 → 1 → 4 … heraus.
Das Problem
- Beobachtung: Egal, mit welcher Zahl du startest – bisher alle getesteten Zahlen landen irgendwann in dieser 4-2-1-Schleife.
- Offene Frage: Kann man beweisen, dass das für alle Zahlen gilt?
- Bisher wurde es mit Computern für unfassbar große Zahlen überprüft (bis weit über 10201020), aber ein allgemeiner Beweis fehlt.
Warum ist das so schwe
- Die Vorschrift mischt Multiplikation (mit 3), Addition (+1) und Teilung (/2). Das führt zu einem chaotischen Verhalten.
- Es ist unvorhersehbar: Manche Startwerte fallen schnell in die 4-2-1-Schleife, andere „wandern“ lange durch sehr große Werte.
- Beispiel: Für n=27n=27 dauert es 111 Schritte, und die Folge steigt erst auf über 9000, bevor sie runterkommt.
- Es sieht einfach aus, enthält aber Strukturen, die stark an Chaos und Dynamiksysteme erinnern.
Was kann man damit machen?
- Selber experimentieren: Du kannst Folgen für verschiedene Startwerte aufschreiben oder programmieren. Das macht das Problem sehr anschaulich.
- Zahlenmuster suchen: Viele Mathematiker und Hobbyforscher untersuchen, welche Zahlen besonders lange brauchen, oder ob man Teilmengen (z. B. alle Zweierpotenzen) erklären kann.
- Verbindung zur Forschung: Das Collatz-Problem berührt Gebiete wie Zahlentheorie, Dynamische Systeme, sogar Kryptographie.
Kurz gesagt:
- Warum es „so ist“, weiß keiner – das ist ja genau das Rätsel.
- Was du machen kannst: damit spielen, Muster suchen, eigene Programme schreiben, und dabei erleben, wie aus einer simplen Regel extrem komplexes Verhalten entstehen kann.

