Was ist die Fibonacci-Folge?
Die Fibonacci-Folge ist eine unendliche Zahlenreihe. Sie wird so definiert:
- Die ersten beiden Zahlen sind 0 und 1.
- Jede weitere Zahl ist die Summe der beiden vorhergehenden Zahlen.
Formal:
F(0) = 0
F(1) = 1
F(n) = F(n−1) + F(n−2) für n ≥ 2
Beispiel:
- 0, 1
- 0 + 1 = 1
- 1 + 1 = 2
- 1 + 2 = 3
- 2 + 3 = 5
- 3 + 5 = 8
- 5 + 8 = 13
- …
Die Folge sieht so aus:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
Mathematische Bedeutung
Die Fibonacci-Folge ist berühmt, weil sie sehr einfache Regeln hat, aber reichhaltige Strukturen zeigt. Sie wird oft genutzt für:
- Rekursion: Die Definition hängt von sich selbst ab. Das macht sie zu einem Lehrbeispiel in der Informatik.
- Zahlentheorie: Sie hat viele interessante Eigenschaften, z. B. teilt jede k-te Fibonacci-Zahl bestimmte andere Fibonacci-Zahlen.
- Binet-Formel: Es gibt eine geschlossene Formel mit Wurzeln, die jede Fibonacci-Zahl direkt berechnet.
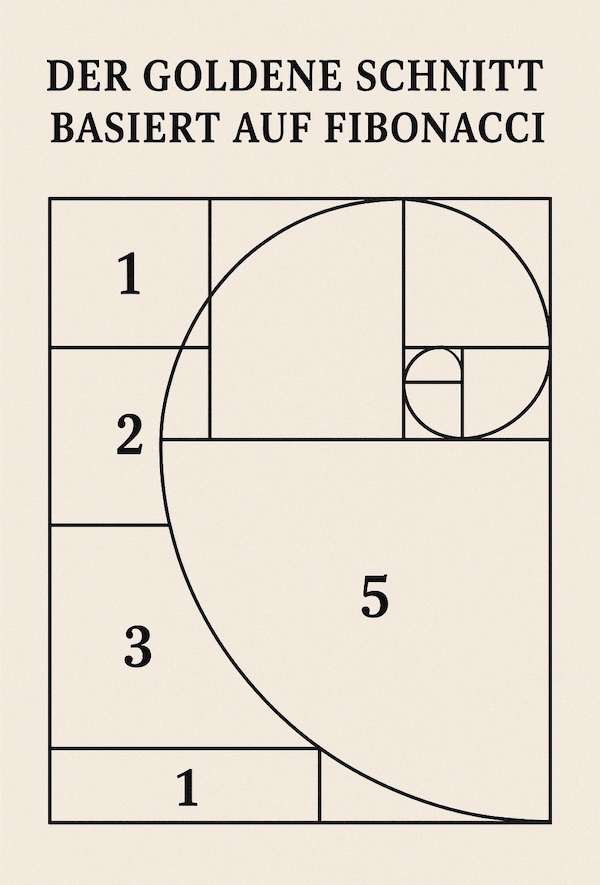
Verbindung zum Goldenen Schnitt
Die Fibonacci-Folge ist eng mit dem Goldenen Schnitt (φ ≈ 1.618) verknüpft:
- Je weiter man in der Folge geht, desto näher kommt das Verhältnis zweier aufeinanderfolgender Zahlen an φ.
Das erklärt, warum Fibonacci-Zahlen und Goldener Schnitt oft zusammen in Kunst und Natur vorkommen.
Vorkommen in der Natur
Die Folge beschreibt Wachstumsprozesse und Muster. Beispiele:
Pflanzenwachstum (Phyllotaxis)
- Blätter ordnen sich oft spiralförmig in Fibonacci-Mustern, sodass jedes Blatt genug Licht bekommt.
- Z. B. 3/5 oder 5/8 Spiralen auf Sonnenblumen.
Samenverteilungen
- Sonnenblumenkerne bilden gegenläufige Spiralen in Fibonacci-Zahlen (z. B. 34 und 55 Spiralen).
Tannenzapfen und Ananas
- Spiralen in Fibonacci-Zahlen (oft 8 und 13).
Schneckenhäuser
- Spiralförmiges Wachstum folgt näherungsweise dem Goldenen Schnitt.
Tierpopulationen
- Fibonacci nutzte die Folge ursprünglich, um Kaninchenpopulationen (idealisiert) zu beschreiben.
Anwendungen in Technik und Informatik
Rekursive Algorithmen
- Fibonacci ist das klassische Beispiel für Rekursion.
Datenstrukturen
- Fibonacci-Heaps (eine effiziente Struktur für Prioritätswarteschlangen).
Computer-Grafik
- Spiralmuster und natürliche Anordnungen werden mit Fibonacci-Werten modelliert.
Verschlüsselung & Codierung
- Einige Codes nutzen Fibonacci-Folgen zur Strukturierung.
Kunst, Architektur und Musik
Komposition
- Viele Künstler gestalten Proportionen nach dem Goldenen Schnitt.
- Da Fibonacci-Zahlen approximativ φ erzeugen, verwenden sie diese als Leitlinie.
Architektur
- Viele klassische Bauwerke (z. B. das Parthenon) zeigen Proportionen, die nahe am Goldenen Schnitt liegen.
Musik
- Takte und Phrasen sind manchmal in Fibonacci-Längen unterteilt.
- Komponisten wie Bartók und Debussy nutzten diese Struktur.
Historisches
- Benannt nach Leonardo von Pisa, genannt Fibonacci (ca. 1170–1240).
- Er stellte die Folge 1202 in seinem Buch „Liber Abaci“ vor, um das Wachstum einer idealisierten Kaninchenpopulation zu modellieren.
- Die Idee war zwar schon früher bekannt (z. B. in Indien), aber Fibonacci machte sie in Europa berühmt.
Zusammenfassung in einem Satz
Die Fibonacci-Folge ist eine unendliche Zahlenreihe, bei der jede Zahl die Summe der beiden vorherigen ist. Sie beschreibt Wachstumsmuster in Natur, Kunst und Technik und steht in engem Bezug zum Goldenen Schnitt.

