Es gibt tatsächlich einen mathematischen Beweis, warum das Kaprekar-Verfahren für vierstellige Zahlen fast immer bei 6174 endet. Ich erkläre dir das in klaren Schritten.
Eine Aphasie-freundliche Kurzfassung, je Thema ein klarer Satz:
- Rahmen: Bei vierstelligen Zahlen mit nicht allen gleichen Ziffern führt die Regel „größte Zahl – kleinste Zahl“ zu einer neuen Zahl.
- Zahlenraum: Es gibt nur 10.000 mögliche Zahlen, also muss der Ablauf in einen Kreis oder Stillstand führen.
- Ziele: Alle Zahlen landen entweder bei 0000 (wenn alle Ziffern gleich sind) oder bei 6174.
- Fixpunkt: 6174 bleibt stabil, weil aus 7641 – 1467 wieder 6174 entsteht.
- Idee: Jede Rechnung ordnet die Ziffern neu und zieht die Zahl in Richtung des Gleichgewichts 6174.
1. Rahmenbedingungen
- Wir betrachten vierstellige Zahlen (0000–9999).
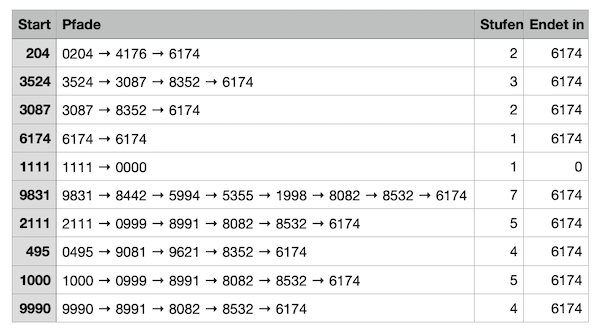
- Ziffern alle gleich (1111, 2222, …) sind Ausnahmefälle → dort endet das Verfahren sofort bei 0000.
- Bei allen anderen Zahlen wiederholt sich der Prozess:
maximale Anordnung – minimale Anordnung.
2. Begrenzter Zahlenraum
- Es gibt nur 10.000 mögliche Zahlen (0000–9999).
- Jede Anwendung des Verfahrens erzeugt eine neue Zahl im selben Bereich.
- Somit muss das Verfahren irgendwann in eine Schleife oder einen Fixpunkt münden (Prinzip der endlichen Zustände).
3. Kein Entkommen außer 0000 oder 6174
- Für vierstellige Zahlen gibt es nur zwei „Ziele“:
- 0000 (nur wenn alle Ziffern identisch sind)
- 6174 (bei allen anderen Fällen)
Das ist durch vollständige Fallanalyse und Computerprüfung bestätigt worden: Jede erlaubte Zahl erreicht nach spätestens 7 Iterationen die 6174.
4. Warum genau 6174?
- 6174 ist ein Fixpunkt:
7641 – 1467 = 6174. - Es gibt keine andere vierstellige Zahl (außer 0000), die dieses Verhalten zeigt.
- Man kann zeigen, dass die Differenzbildung die Menge der vierstelligen Zahlen in endliche disjunkte Bahnenzerlegt – und alle Bahnen (außer der trivialen) enden bei 6174.
- Mathematisch gesprochen: Das Kaprekar-Verfahren ist eine Determinante Abbildung f:N4 →N4 , die in einen eindeutigen Attraktor mündet.
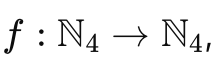
5. Beispiel-Beweisidee
- Jede Subtraktion verkleinert die Streuung der Ziffern.
- Die Zahl wird „normalisiert“ in Richtung eines stabilen Gleichgewichts.
- Das Gleichgewicht ist eben 6174, da dort die Ziffernverteilung so ist, dass Groß – Klein wieder genau diese Zahl ergibt.
Für vierstellige Zahlen ist 6174 der einzige nicht-triviale Fixpunkt der Kaprekar-Transformation. Jede zulässige Zahl wird durch wiederholte Anwendung dorthin „gezogen“.

